Math

Determine Whether a Given Ordered Pair is a Solution of an Equation

 4 of 5 

In mathematics we frequently have an equation or formula that relates two variables. Think about a square. We have the perimeter and the length of a side. We are relating the two variables and evaluating the perimeter with the formula P = 4x. We could evaluate the area, A, using the formula A = x².

Remember that a variable can represent any number, so in this lesson we will only be using the variables x and y (not variables like P and A). We will write y = 4x instead of P= 4x or y = x² instead of A = x².

Using the variables x and y, we will learn how to find a solution to the equation by identifying if an ordered pair satisfies the equation, that is, which makes the equation true.

Instructions: Complete each ordered pair solution of the given equations.

Look at another example. This time we will use a table.

y = 4x.

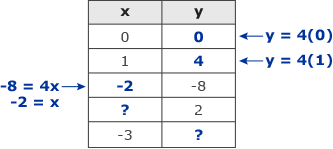
Beneath the equation we have a table with the left column headed x and the right column headed y. In the x column we have 0 (typed), 1 (typed) ,-2 (handwritten with -8 = 4x and -2 = x written next to it to the left), (handwritten, and -3 typed). In the y column we have 0 (handwritten with y = 4(0) next to it to the right), 4 (handwritten with y = 4(1) next to it to the right), -8 (typed), 2 (typed), and handwritten.

Work is shown alongside the table above for the first four ordered pairs. Some of its solutions are the ordered pairs (0,0), (1,4), and (-2, -8). Let's work out the last two now.

• y = 4x
• 2 = 4x Substitute the number 2 for y on the left side of the equation.
• $\frac{1}{2}$ = x The result of dividing both sides of the equation by 4.

The above steps show how to obtain the solution ($\frac{1}{2}$, 2) that was in the list of four solutions to the equation.

To obtain more solutions we could continue the process. Now we shall use -3 as the value of x as shown in the table above. Our equation is
y = 4x
y = 4(-3)
y = -12

So we now have a new solution (-3, -12).

There are infinitely many solutions to an equation like this. Notice that when we write the equation, it is possible to have x and y values that are any real numbers, positive, negative or zero. However, when we apply the equation to a specific situation, like the perimeter or area of a square, we would only consider solutions that fit that situation or application.